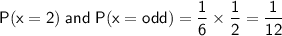Question

You roll a six-sided die twice. What is the probability of rolling a 2 and then an odd number?

A1/18
B 1/6
C1/3
D1/12

Answer 1

`\textsf{D)} \quad (1)/(12)`

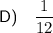
Explanation:

Probability is a measure of how likely events are to happen.

When all the possible outcomes are equally likely, we can use this formula to calculate the probability of an event happening:

`\boxed{\sf P(event)=\frac{\textsf{Number of outcomes where event happens}}{\textsf{Total number of possible outcomes}}}`

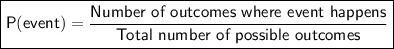
There are 6 sides on the dice numbered 1 through 6.

Therefore, the total number of possible outcomes is 6.

Assuming the dice is fair, the probability of rolling a 2 is:

`\sf P(x=2)=(1)/(6)`

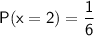
There are 3 odd numbers in the set of numbers {1, 2, 3, 4, 5, 6}.

Therefore, the probability of rolling an odd number is:

`\sf P(x=1)\;or\;P(x=3)\;or\;P(x=5)=(1)/(6)+(1)/(6)+(1)/(6)=(3)/(6)=(1)/(2)`

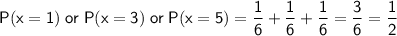
Therefore, the probability of rolling a 2 and then an odd number is:

`\sf P(x=2)\;and\;P(x=odd)=(1)/(6) * (1)/(2)=(1)/(12)`

Answer 2

answer : D1/12

steps:

'and' in a word problem means multiply

rolling a 2 : 1/6

odd :

1 2 3 4 5 6

1 3 5 are 3 odd numbers so

3/6 which is 1/2

1/6 * 1/2 = 1/12