Question

Please show step by step and state whether the solutions are real or complex

Answer 1

real

Explanation:

To determine whether the solutions are real or complex, use the discriminant which is given by
`b^2-4ac.`

With the given equation, a=1, b=3, and c=-10. Substituting the values of a, b, c in the expression for the discriminant results in

`\begin{aligned}\\b^2-4ac&=3^2-4(1)(-10)\\&=9+40\\&=49.\end{aligned}`

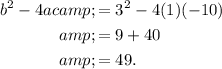
Since the value of the discriminant is a positive number, then the solutions of the given quadratic equation are real. (Note that if the discriminant were a negative number, then the solutions are complex.)

Answer 2

x= 5

x= -2

Explanation:

Write your equation in factored form

(x-5)(x+2)= 0

Set each factor equal to zero

x-5= 0

x+2= 0

Rearrange and isolate the variable to find each solution

x= 5

x= -2