Answer:
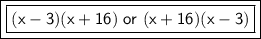
Solution Steps:
______________________________
1.) Factor the expression by grouping:
- First, the expression needs to be rewritten as
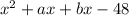 . To find a and b, set up a system to be solved:
. To find a and b, set up a system to be solved:
2.) List all such integer pairs that give product −48:
3.) Calculate the sum for each pair:
4.) The solution is the pair that gives sum 13:
5.) Rewrite
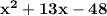 :
:
6.) Factor out
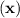 in the first and 16 in the second group:
in the first and 16 in the second group:
7.) Factor out common term
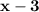 by using distributive property:
by using distributive property:
So your answer is
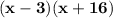 or
or
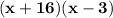 .
.
______________________________