Question

Diagram 3 shows a trapezium.
Given the area of trapezium is (4x+4) cm². Find the value of x. ​

Answer 1

B) 4

Explanation:

The formula for calculating the area of a trapezium:

`area = (a + b)/(2) * h`

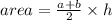
Where a and b are parallel sides and is the height.

a = 2x+3

b = 3-x

h = x

area = 4x+4

Substitute these values in the equation:

`4x + 4 = ((2x+3+3-x)/(2) )×x`

`4x + 4 = ( (x + 6)/(2) ) * x`

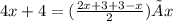
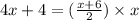
Now multiply the numerator (x+6) with x:

`4x + 4 = \frac{x {}^(2) + 6x }{2}`

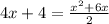
Multiply both sides by 2 which cancels out the fraction on the right:

`2(4x + 4) = x {}^(2) + 6x`

`8x + 8 = x {}^(2) + 6x`

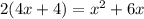
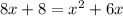
Bring 8x and 8 to the right by subtracting them on both sides:

`8x + 8 - 8x - 8 = x {}^(2) + 6x - 8x - 8`

`0 = x {}^(2) + 6x - 8x - 8`

`0 = {x}^(2) - 2x - 8`

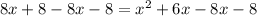
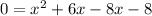
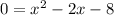
Now we can solve for x by factorising:

What two numbers multiply to make -8 and add to make -2? The two numbers are -4 and 2, so we can factor it as:

`0 = (x - 4)(x + 2)`

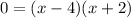
Solving for the first solution :

`(x - 4) = 0`

`x = 4`

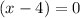
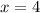
Solving for the second solution:

`(x + 2) = 0`

`x = - 2`

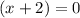
x is equal to 4 and -2, however, we cannot have a negative length of -2

Hence x = 4