Question

Consider the polynomial g(x)=2x^3+2x^2-28x-48List all the zeros and their muliplicities

Answer 1

To find all the zeros of a polynomial, we have to factor it completely. We'll have a series of factors in the form:

`(x-a)`

Were a is a zero of the polynomial.

Let's find the zeros of the given polynomial:

`2x^3+2x^2-28x-48`
`\begin{gathered} \rightarrow2(x+2)(x+3)(x-4) \\ \rightarrow2(x-(-2))(x-(-3))(x-4) \end{gathered}`

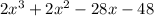
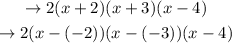
Thereby, the zeros of the polynomial are -2, -3 and 4. Each one with a multiplicity of one (They appear only one time)