Question

Triangle ABC can be plotted at A (-14, 14), B (-8, 11) & C (-14, 5). Reflect Triangle ABC across the y-axis. Next, rotate 180 degrees counterclockwise about the origin. What is the ordered pair of C'' after the sequence of transformations?

Answer 1

Answer: (-14,-5)

=======================================================

Step-by-step explanation:

The y-axis reflection rule is

`(\text{x},\text{y}) \to (-\text{x},\text{y})`

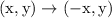
The x coordinate flips in sign from positive to negative, or vice versa. The y coordinate stays the same.

A point like C(-14,5) will then reflect to...

`(\text{x},\text{y}) \to (-\text{x},\text{y})\\\\(-14,5) \to (-(-14),5)\\\\(-14,5) \to (14,5)`

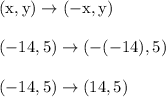
So we have point C' located at (14,5) after applying the y-axis reflection rule on point C.

-------------

The next operation to do is is the 180 degree rotation. This can be clockwise or counterclockwise. That rotation rule is

`(\text{x},\text{y}) \to (-\text{x},-\text{y})`

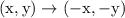
This time both coordinates flip in sign. This rule only works if the center of rotation is the origin.

Let's apply that rotation rule to C' to find where C'' is located.

`(\text{x},\text{y}) \to (-\text{x},-\text{y})\\\\(14,5) \to (-14,-5)\\`

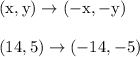
Therefore, the point C'' is located at (-14,-5)

See the diagram below.