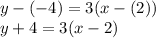Answer (assuming it can be put in point-slope format):
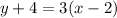
Explanation:
You can write an equation of a line when knowing its slope and a line it passes through using point slope formula,
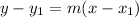 .
.
1) First, find the slope of the equation. We know it has to be parallel to y = 3x + 2. Lines that are parallel have the same slope, thus the slope of y = 3x + 2 is the slope of the answer as well. y = 3x + 2 is in slope-intercept format, or
 . The coefficient of the x term, or
. The coefficient of the x term, or
 , represents the slope - so, the slope must be 3.
, represents the slope - so, the slope must be 3.
2) Now, use point-slope formula,
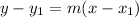 , to write the equation. Substitute
, to write the equation. Substitute
 ,
,
 , and
, and
 for real values.
for real values.
The
 represents the slope, so substitute 3 for
represents the slope, so substitute 3 for
 . The
. The
 and
and
 represent the x and y values of a point the line crosses through. The line crosses through (2, -4), so substitute 2 for
represent the x and y values of a point the line crosses through. The line crosses through (2, -4), so substitute 2 for
 and -4 for
and -4 for
 . This gives the following answer:
. This gives the following answer: