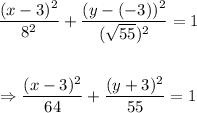Answer:
The equation of the ellipse is:

Explanation:
Remember that the general equation of an ellipse is:
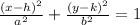
Where:
• (h,k), are the coordinates of the center
,
• a, is the major axis lenght
,
• b, is the minor axis lenght
We also have that the equation for the foci is:
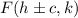
And we also have that:
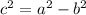
Since we have two foci, we can find the values of h and c as following:
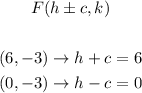
We'll have the following system of equations:
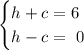
Adding up both equations and solving for h,
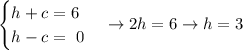
Using this h value in the first equation and solving for c,
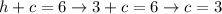
We'll have that the solution to this particular system of equations is:
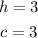
Now we know the value of c we can calculate the value of b as following:
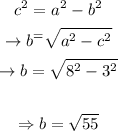
With all these calculations, we'll have all the values we need to put together the equation:

This way, we'll have that the equation of the ellipse is: