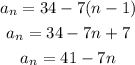Question

A_8=-15, A_17=-78 write a rule for the nth term of the arithmetic sequence.

Answer 1

a(n)=41-7n

Step-by-step explanation:

The nth term of an arithmetic sequence is obtained using the formula:

`\begin{gathered} a_n=a_1+(n-1)d \\ a_1=\text{first term},d=\text{common difference} \end{gathered}`

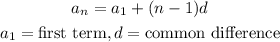
Given:

`\begin{gathered} a_8=-15\implies a_1+(8-1)d=-15 \\ \implies a_1+7d=-15\ldots(1) \\ a_(17)=-78\implies a_1+(17-1)d=-78 \\ \implies a_1+16d=-78\ldots(2) \end{gathered}`

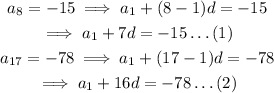
Solve the equations labeled (1) and (2) simultaneously:

`\begin{gathered} a_1+7d=-15\ldots(1) \\ a_1+16d=-78\ldots(2) \\ \text{Subtract (1) from (2):} \\ 16d-7d=-78-(-15) \\ 9d=-63 \\ \text{Divide both sides by 9} \\ (9d)/(9)=(-63)/(9) \\ d=-7 \end{gathered}`

Substitute d=-7 into equation 1 to solve for a1.

`\begin{gathered} a_1+7d=-15\ldots(1) \\ a_1+7(-7)=-15 \\ a_1-49=-15 \\ a_1=-15+49 \\ a_1=34 \end{gathered}`

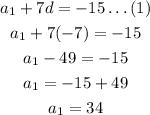
Therefore, a rule for the nth term of the arithmetic sequence:

`\begin{gathered} a_n=34-7(n-1) \\ a_n=34-7n+7 \\ a_n=41-7n \end{gathered}`