Question

Questions Below. Would Appreciate Help!

Answer 1

The function that could be the function described is;

`f(x) = -10 \cdot cos \left ((2 \cdot \pi )/(3) \cdot x \right ) + 10`

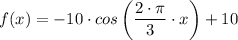
Explanation:

The given parameters of the cosine function are;

The period of the cosine function = 3

The maximum value of the cosine function = 20

The minimum value of the cosine function = 0

The general form of the cosine function is presented as follows;

y = A·cos(ω·x - ∅) + k

Where;

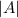`\left | A \right |` = The amplitude = Constant

The period, T = 2·π/ω

The phase shift, = ∅/ω

k = The vertical translation = Constant

Therefore, by comparison, we have;

T = 3 = 2·π/ω

∴ ω = 2·π/3

The range of value of the cosine of an angle are;

-1 ≤ cos(θ) ≤ 1

Therefore, when A = 10, cos(ω·x - ∅) = 1 (maximum value of cos(θ)) and k = 10, we have;

y = A × cos(ω·x - ∅) + k

y = 10 × 1 + 10 = 20 = The maximum value of the function

Similarly, when A = 10, cos(ω·x - ∅) = -1 (minimum value of cos(θ)) and k = 10, we get;

y = 10 × -1 + 10 = 0 = The minimum value of the function

Given that the function is a reflection of the parent function, we can have;

A = -10, cos(ω·x - ∅) = -1 (minimum value of cos(θ)) and k = 10, to get;

y = -10 × -1 + 10 = 20 = The maximum value of the function

Similarly, for cos(ω·x - ∅) = 1 we get;

y = -10 × 1 + 10 = 0 = The minimum value of the function

Therefore, the likely values of the function are therefore;

A = -10, k = 10

The function is therefore presented as follows;

y = -10 × cos(2·π/3·x) + 10