Question

The graph of a polynomial function of degree 5 has three x-intercepts, all with multiplicity 1. Describe the nature and number of all its zeros.

A) The function has 5 real zeros. B) The function has 3 real zeros. C) The function has 3 real and 2 imaginary zeros. D) The function has 2 real and 3 imaginary zeros.

Answer 1

I think the answer is C. It does have 3 zeros (as B also says) but since it is a 5th degree polynomial, it must have 5 zeros. Since the other 3 are multiplicity 1, 2 of the zeros are imaginary.

Answer 2

For this case suppose that we have a polynomial in its standard form of the form:

`image`

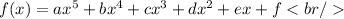
Where,

a, b, c, d, e, f: coefficients of the polynomial

x: independent varible

f (x): dependent variable

Since the polynomial is of degree 5, then the polynomial has 5 solutions that comply with:

`image`

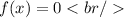
We know that three of the solutions are real and are repeated only once.

Therefore, the two remaining solutions are complex numbers.

Answer:

C) The function has 3 real and 2 imaginary zeros.