Question

I need help with this maze assignment about segments

Answer 1

(1) T, U and V are collinear which means they all lie on the same line segment.

Suppose U is between T and V and that TU = 7x - 4, and UV = 6x + 10 and TV = 45, find TU.

`\begin{gathered} TV=TU+UV \\ 45=7x-4+6x+10 \\ 45=7x+6x+10-4 \\ 45=13x+6 \\ 45-6=13x \\ 39=13x \\ \text{Divide both sides by 13} \\ 3=x \\ \text{If TU is 7x - 4, then} \\ TU=7(3)-4 \\ TU=21-4 \\ TU=17 \end{gathered}`

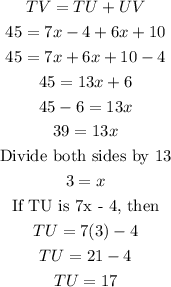
(2) Angles LMN + NMO + OMP = 180 (Angles on a straight line equals 180

`\begin{gathered} 4x+2x+90=180 \\ 6x+90=180 \\ 6x=180-90 \\ 6x=90 \\ \text{Divide both sides by 6} \\ x=15 \\ \text{Therefore, if angle LMN is 4x, then} \\ \angle LMN=4x \\ \angle LMN=4(15) \\ \angle LMN=60 \end{gathered}`

(3) If on the line segment, Ef is 3x and FG is three times as long as EF, then FG is 3x times 3 which is 9x. Hence, you now have;

`\begin{gathered} EF+FG=EG \\ 3x+9x=72 \\ 12x=72 \\ \text{Divide both sides by 12} \\ x=6 \\ \text{If FG is 9x, then} \\ FG=9x \\ FG=9(6) \\ FG=54 \end{gathered}`

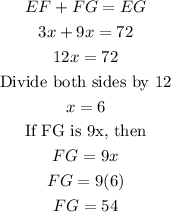
(4) If WZ = 32, and YZ = 6, that means WY is derived as

`\begin{gathered} WY+YZ=WZ \\ WY+6=32 \\ \text{Subtract 6 from both sides} \\ WY=26 \\ \text{If X is the midpoint of WY, then} \\ WX=(WY)/(2) \\ WX=(26)/(2) \\ WX=13 \end{gathered}`

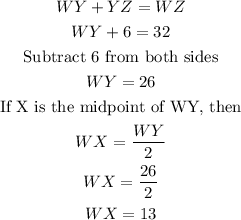
(5) Angles A and B are complementary, which means they both add up to 90 degrees. Therefore;

`\begin{gathered} (x-4)+(2x+7)=90 \\ x-4+2x+7=90 \\ x+2x+7-4=90 \\ 3x+3=90 \\ \text{Subtract 3 from both sides;} \\ 3x=87 \\ \text{Divide both sides by 3} \\ x=29 \end{gathered}`

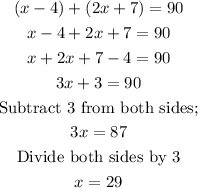
(6) Angle XWY = 83, and angle YWZ = 34. Angle XWZ is a combination of XWY and YWZ, therefore;

`\begin{gathered} \text{XWZ}=\text{XWY}+\text{YWZ} \\ \text{XWZ}=83+34 \\ \text{XWZ}=117 \end{gathered}`

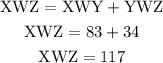
(7) If Line segment QS = 23, and QR = 7, then;

`\begin{gathered} QR+RS=QS \\ 7+RS=23 \\ \text{Subtract 7 from both sides} \\ RS=16 \end{gathered}`

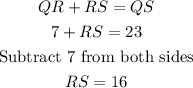
(8) If angle RSU = 76, observe that angles RST plus TSU equals angle RSU.

Therefore;

`\begin{gathered} \angle RST+\angle TSU=RSU \\ 7x+8+3x-2=76 \\ 7x+3x+8-2=76 \\ 10x+6=76 \\ \text{Subtract 6 from both sides} \\ 10x=70 \\ \text{Divide both sides by 10} \\ x=7 \end{gathered}`

(9) If line segment JL measures 10x + 7, and line segment JK and KL added together equals line segment JL, then;

`\begin{gathered} 9x-11+5x+2=10x+7 \\ 9x+5x-11+2=10x+7 \\ \text{Collect like terms and you have} \\ 9x+5x-10x=7+11-2 \\ \text{Note that when positive numbers cross the equation} \\ \text{they become negative, and vice versa for negative numbers} \\ 4x=16 \\ \text{Divide both sides by 4} \\ x=4 \\ \text{Therefore, JK measures} \\ JK=9x-11 \\ JK=9(4)-11 \\ JK=36-11 \\ JK=25 \end{gathered}`

(10) Angles on a straight line equals 180, that means angle ABC plus angle CBD equals 180.

`\begin{gathered} \angle ABC+\angle CBD=180 \\ 13x-20+7x=180 \\ 13x+7x-20=180 \\ 20x-20=180 \\ \text{Add 20 to both sides} \\ 20x=200 \\ \text{Divide both sides by 20} \\ x=10 \\ \text{Therefore,} \\ \angle ABC=13x-20 \\ \angle ABC=13(10)-20 \\ \angle ABC=130-20 \\ \angle ABC=110 \end{gathered}`

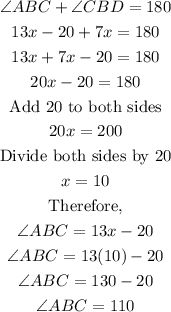
(11)