Question

For which of the following intervals does the function (in the image section) have a removable discontinuity?A. [−2.5,−1.5] B. [−1.5,−0.5] C. [−0.5,0.5] D. [0.5,1.5] E. [1.5,2.5]

Answer 1

Given the function below,

`f(x)=(x+2)/(x^4-2x^3-x^2+2x)`

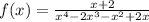
Let us now factorize the denominator

`x^4-2x^3-x^2+2x`

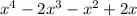
First of all, let us factorize x out from the denominator.

`\begin{gathered} x((x^4)/(x)-(2x^3)/(x)-(x^2)/(x)+(2x)/(x)) \\ x(x^3-2x^2-x+2) \end{gathered}`

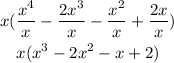
Therefore, x is a factor of the denominator.

Let us now factorize the remainder

`x^3-2x^2-x+2`

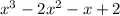
Let us substitute x = 1 into the function to confirm if it is a factor.

`\begin{gathered} x=1 \\ 1^3-2(1)^2-(1)+2 \\ 1-2-1+2=1+2-1-2=3-3=0 \end{gathered}`

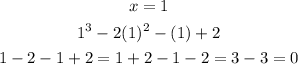
Therefore, (x - 1) is a factor.

Let us now divide the function by (x - 1)

`(x^3-2x^2-x+2)/(x-1)=(\left(x-2\right)\left(x+1\right)\left(x-1\right))/(x-1)=(x-2)(x+1)`

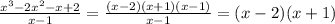
Hence, the factors of the denominator are,

`x(x-1)(x+1)(x-2)`

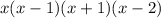
Therefore,

`f(x)=(x+2)/(x(x-1)(x+1)(x-2))`

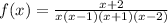
Now, looking at both the numerator and the denominator, we can observe that there is no common factor between the numerator and the denominator.

Hence, there is no removable discontinuity.