Question

The length of the longer leg of a right triangle is three less than twice the length of the shorter leg, and the length of the hypotenuse is five more than twice the length of the shorter leg. If the length of the shorter leg is k, write an equation to find the value of k

Answer 1

length of the shorter leg = k

length of the longer leg = 2k - 3

length of the hypothenus = 5 + 2k

to solve this problem, we have to use pythagorean theorem

pythagorean theorem states that

`\text{hyp}^2=\text{adj}^2+\text{opp}^2`

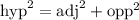
hyp = hypothenus

adj = adjacent

opp = opposite

now let's plug in our variables into the equation

`(5k+2)^2=(2k-3)^2+k^2`

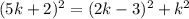
this is an equation to find the value of k

we can further simplify this to get a quadratic equation

`\begin{gathered} (5k+2)^2=(2k-3)^2+k^2_{} \\ 10k^2+20k+4=(4k^2-12k+9)+k^2 \\ 10k^2+20k+4=4k^2-12k+9+k^2 \\ \text{collect like terms} \\ 10k^2+20k+4-4k^2+12k-9-k^2 \\ (10-4-1)k^2+(20+12)k-9+4_{} \\ 5k^2+32k-5=0 \end{gathered}`

the above written equation can be used to solve for k

note: in opening the bracket