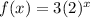Answer
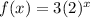
Explanation
To solve this, we re using the standard exponential equation:

Also, remember that
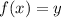
We know that our exponential function goes through the points (1, 6) and (2, 12), so we are going to replace the points in our stander exponential equation and solve for
 and
and
 :
:
For (1, 6)
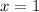 and
and
 , so:
, so:

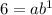
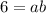
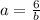 equation (1)
equation (1)
For (2, 12)
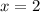 and
and
 , so:
, so:

 equation (2)
equation (2)
Replace equation (1) in equation (2) and solve for b

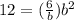
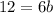

 equation (3)
equation (3)
Replace equation (3) in equation (1) to find a
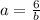
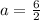
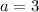
Now we can complete our exponential function:

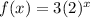
We can conclude that the exponential function that goes through the points (1, 6) and (2, 12) is