Question

Solve the following for 'x'x+1+3 2= xO A. -1O B. 3O c. 3OD. 1

Answer 1

Finding x

Step 1: "braking" fractions

`\begin{gathered} (x)/(3)+(x+1)/(2)=x \\ (x+1)/(2)=(x)/(2)+(1)/(2) \end{gathered}`

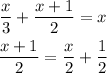
We replace the second in the original equation:

`(x)/(3)+(x)/(2)+(1)/(2)=x`

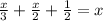
Step 2: rearraging the equation (the terms with x on one side, numbers on the other)

`\begin{gathered} (x)/(3)+(x)/(2)+(1)/(2)=x \\ (x)/(3)+(x)/(2)=x-(1)/(2) \\ (x)/(3)+(x)/(2)-x=-(1)/(2) \end{gathered}`

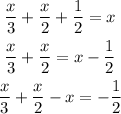
Step 3: adding fractions

Since

`\begin{gathered} (1)/(3)+(1)/(2)-1=(1)/(3)+(1)/(2)-(1)/(1) \\ =((1)/(3)+(1)/(2))-(1)/(1) \\ \end{gathered}`

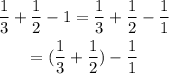
We know that

`\begin{gathered} ((1)/(3)+(1)/(2))=(1\cdot2+1\cdot3)/(3\cdot2) \\ =(2+3)/(6) \\ =(5)/(6) \end{gathered}`

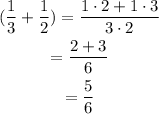
Replacing it:

`\begin{gathered} ((1)/(3)+(1)/(2))-(1)/(1)=(5)/(6)-(1)/(1) \\ =(5\cdot1-6\cdot1)/(6\cdot1) \\ =(5-6)/(6) \\ =-(1)/(6) \end{gathered}`

Then

`\begin{gathered} (x)/(3)+(x)/(2)-x=-(1)/(2) \\ -(1)/(6)x=-(1)/(2) \end{gathered}`

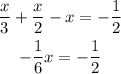
Step 4: finding x

`\begin{gathered} -(1)/(6)x=-(1)/(2) \\ (1)/(6)x=(1)/(2) \\ 6\cdot(1)/(6)x=6\cdot(1)/(2) \\ x=3 \end{gathered}`

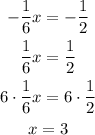
Answer: C.x=3