Question

700 tickets were sold for a game for a total of $900.00 If adult tickets sold for $2.00 and children's tickets sold for $1.00 how many of each kind of ticket were sold?

Answer 1

Let x be the number of adult tickets and let y be the number of children.

We know that in total there were sold 700 tickets, that means:

`x+y=700`

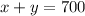
Now we know that each adult ticket was $2 and the children's tickets was $1, and that the total was $900, this means that:

`2x+y=900`

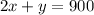
Then we have the following system of equations:

`\begin{gathered} x+y=700 \\ 2x+y=900 \end{gathered}`

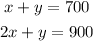
To solve it we substract the second equation from the first one, then we have:

`\begin{gathered} x+y-2x-y=700-900 \\ -x=-200 \\ x=200 \end{gathered}`

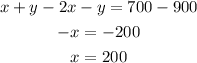
Now that we have the value of x we plug it in the first equation to find y:

`\begin{gathered} 200+y=700 \\ y=700-200 \\ y=500 \end{gathered}`

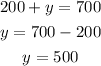
Therefore, there were 200 adult's tickets and 500 children's tickets sold.