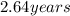Question

A radioactive substance decays so that after t years, the amount remaining, expressed as a percent of the original amount, is A(t)=100(1.3)^-tWhat is the Half-Life of this substance?

Answer 1

Step-by-step explanation:

The dunction is given below as

`A(t)=100(1.3)^(-t)`

To figure out the half life,

The new mass of the decayed substance will be half that of the initial substance

`\begin{gathered} A(t)=100\left(1.3\right)^(-t) \\ A(t)=(100)/(2)=50 \end{gathered}`

By substituting the values, we will have

`\begin{gathered} A(t)=100(1.3)^(-t) \\ 50=100(1.3)^(-t) \\ (50)/(100)=1.3^(-t) \\ (1)/(2)=1.3^(-t) \end{gathered}`

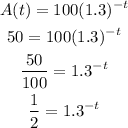
Apply exponent rules

`\begin{gathered} (1)/(2)=1.3^(-t) \\ ln((1)/(2))=-tln(1.3) \\ t=(ln(2))/(ln(1.3)) \\ t=2.64years \end{gathered}`

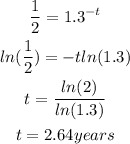
Hence,

The final answer is

`2.64years`