Question

What is the acceleration due to gravity at the surface of a planet that is twice as dense as the earth, but whose radius is twice as large as the earth’s? Assume the earth is a perfect sphere with a volume given by 4/3 piR^3.

Answer 1

39.2 m/s^2

Explanation:

We have to acceleration due to gravity at the surface of planet:

`\begin{gathered} g_p=\frac{GM_p}{(R_p)^2^{}},M_p=\rho_p\cdot V_p \\ g_p=(G\cdot\rho_p\cdot V_p)/((R_p)^2) \\ g_p=\frac{G\cdot\rho_p\cdot(4)/(3)\pi(R^3_p)_{}}{(R_p)^2} \\ g_p=(4)/(3)\pi\cdot G\cdot\rho_p\cdot R_p \end{gathered}`

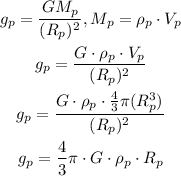
Where,

Mp = mass of planet

ρp = density of planet

Rp = radius of planet

Given:

ρp = 2ρe, Rp = 2Re

where,

ρe = density of earth

Re = radius of earth

Replacing:

`\begin{gathered} g_p=(4)/(3)\pi\cdot G\cdot2\rho_e\cdot2R_e \\ g_p=4\cdot\mleft((4)/(3)\pi\cdot\: G\cdot2\rho_e\cdot2R_e\mright) \\ g_p=4\cdot g_e \\ g_e=9.8m/s^2 \\ \text{ replacing} \\ g_p=9.8\cdot4 \\ g_p=39.2m/s^2 \end{gathered}`

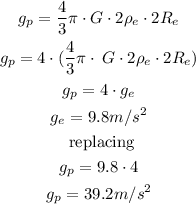
Therefore the acceleration due to gravity on the planet is 39.2 m/s^2