Question

An original sample of the radioisotope fluorine-21 had a mass of 80.0 milligrams. Only 20.0 milligrams of this original sample remain unchanged after 8.32 seconds. What is the half-life of fluorine-21?

(1) 1.04 s (3) 4.16 s
(2) 2.08 s (4) 8.32 s

Answer 1

4.16s

Step-by-step explanation:

N = 20*10⁻³g

N₀ = 80*10⁻³g

t = 8.32

N = N₀e⁻λt

In(N/N₀) = -λt

-λ = 1/t * In(N/N₀)

-λ = 1 / 8.32 * In (20*10⁻³ / 80*10⁻³)

-λ = 0.12 * In(0.25)

-λ = -0.167

λ = 0.167

t½ = 0.693 / λ

t½ = 0.693 / 0.167

t½ = 4.16s

Answer 2

Answer: The correct answer is Option 3.

Step-by-step explanation:

All the radioisotope decay processes follow first order kinetics.

Rate law expression for first order kinetics is given by the equation:

`k=(2.303)/(t)\log(a)/(a-x)`

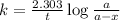
where,

k = rate constant = ?

t = time taken for decay process = 8.32 seconds

a = initial amount of the reactant = 80 mg

a - x = amount left after decay process = 20 mg

Putting values in above equation, we get:

`k=(2.303)/(8.32sec)\log(80g)/(20)\\\\k=0.166sec^(-1)`

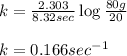
The equation used to calculate half life for first order kinetics:

`t_(1/2)=(0.693)/(k)`

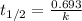
where,

`t_(1/2)` = half life of the reaction = ?

k =
`0.166sec^(-1)`

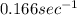
Putting values in above equation, we get:

`t_(1/2)=(0.693)/(0.166sec^(-1))=4.16sec`

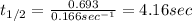
Hence, the correct answer is Option 3.