Question

If there is 360 grams of radioactive material with a half-life of 8 hours, how much of the radioactive material will be left after 32 hours and is the radioactive decay modeled by a linear function or an exponential function?

A. 22.5 grams; linear

B. 22.5 grams; exponential

C.45 grams; linear

D. 45 grams; exponential

Answer 1

B. 22.5 grams; exponential .

Explanation:

We have been given that there is 360 grams of radioactive material with a half-life of 8 hours.

As amount of radioactive material remains 1/2 of the amount after each 8 hours, therefore, our function will be an exponential decay function.

We will use half-life formula to solve our given problem.

`y=a*((1)/(2))^{(t)/(b)}`, where,

`a=\text{Initial value}`,

`t=\text{Time}`,

`b=\text{Half life}`.

Let us substitute a=360 and b=8 in half life formula to get half life function for our given radioactive material.

`y=360*((1)/(2))^{(t)/(8)}`, where y represents remaining amount of radioactive material after t hours.

Therefore, the function
`y=360*((1)/(2))^{(t)/(8)}` gives the half-life of our given radioactive material.

Let us substitute t=32 in our half life function to find the amount of material left after 32 hours.

`y=360*((1)/(2))^{(32)/(8)}`

`y=360*((1)/(2))^(4)`

`y=360*(1^4)/(2^4)`

`y=360*(1)/(16)`

`y=22.5`

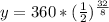
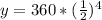
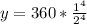
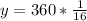
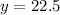
Therefore, the radioactive material will be left 22.5 grams after 32 hours and the radioactive decay is modeled by an exponential function and option B is the correct choice.

Answer 2

B.) 22.5 GRAMS, EXPONENTIAL

32 hours ÷ 8 hours = 4

The radioactive material will half 4 times.

360 x (1/2)⁴ = 22.50

360 x 1/2 = 180
180 x 1/2 = 90
90 x 1/2 = 45
45 x 1/2 = 22.50