Question

If x/y

is rational, must x and y each be rational?
A) Yes; because the quotient of rationals is rational.
B) No; because x and y could have a common irrational factor.
C) No; because the quotient of irrationals is always irrational.
D) Yes; because x and y must be integers, and integers are rational.

Answer 1

Answer: The answer is B.

Explanation:

No; because x and y could have a common irrational factor.

Answer 2

The answer is B.

Consider the fraction
`(6 √(5) )/(√(5))`.

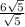
Both the numerator and denominator, when by themselves, are irrational.

However, when they are divided, they result in the rational number
`(6 √(5) )/(√(5))=\boxed{6}`.

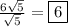
When
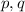
`p,q` have the same irrational factor, the irrational factor will be cancelled from the fraction and (possibly) leave a rational number.