Question

Question 2Which of the following is the solution to the differential equation dP/dt +P=10 with the initial condition P(0) = 4

Answer 1

`\begin{gathered} (dP)/(dt)+P^(\prime)=10 \\ \\ (1)/(10-P)* P^(\prime)=1 \end{gathered}`

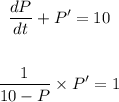
On the left I make the integral with respect to P and on the right the integral with respect to t

`-(\ln (10-P))=t+c`
`\begin{gathered} \ln (10-P)=-t+c \\ \end{gathered}`

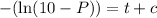
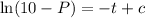
we use e to simplify Steps to constant

`\begin{gathered} e^(\ln (10-P))=e^((-t+c)) \\ 10-P=e^(-t+c) \\ 10-P=e^(-t)* e^c \\ 10-P=e^(-t)* c \\ 10-P=ce^(-t) \end{gathered}`

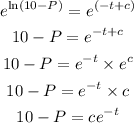
now, solve P

`P=-ce^(-t)+10`

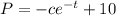
to find c we use P(0)=4, so when we replcae t=0 the soltuion must be 4

`\begin{gathered} 4=-ce^(-0)+10 \\ 4=-c+10 \\ c=10-4 \\ c=6 \end{gathered}`

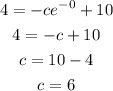
the complete function is

`P=-6e^(-t)+10`

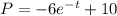
or

`P=10-6e^(-t)`

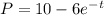
so, the right option is C