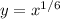ANSWER
C. Power rule
E. Equality rule
Step-by-step explanation
The power rule of logarithms is:
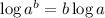
It can be applied in both ways. This means that in this expression we can put the power back:
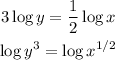
So first we would use the power rule.
Then, we have log on both sides. The equality rule is:
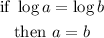
So for this expression:
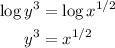
So next we would apply the equality rule.
And then we would finish solving the equation: