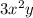Answer:
Greatest common factor of
 and
and
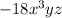 is
is
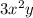
Explanation:
Greatest common factor is the common factor for two or more numbers such that greatest common factor divides both the number.
We find Greatest common factor by
- doing prime factorization and then
- taking common factors from all the factors and
- if they do not have nay term common then Greatest common factor is 1.
Given Numbers are
 and
and
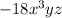
First we do prime factorization of
 .
.
15 can be written as product of prime 3 and 5, so
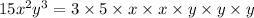
and Similarly,
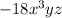 can be written as,
can be written as,
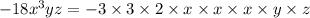
Thus, taking common from both the terms,we get,
Greatest common factor as