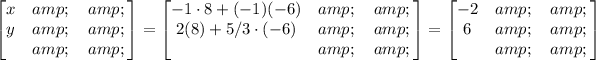Question

Hello it’s showing that I got part of the answer correctNot sure where I went wrong

Answer 1

The A matrix is:

`\begin{bmatrix}{5} & {3} & {} \\ {-6} & {-3} & {} \\ {} & {} & {}\end{bmatrix}`

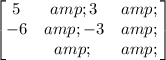
We can write the system of equations in matrix form like this:

`\begin{bmatrix}{5} & {3} & {} \\ {-6} & {-3} & {} \\ {} & {} & {}\end{bmatrix}\cdot\begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{8} & {} & {} \\ {-6} & {} & {} \\ {} & {} & {}\end{bmatrix}`

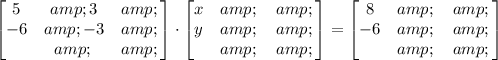
And we can express that as this:

`A\cdot X=B`

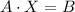
Then the solution is:

`X=A^(-1)\cdot B`

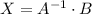
Then, we need to find the inverse of the function to find the solution, start by calculating the determinant:

`\begin{gathered} \text{ Determinant:} \\ d(A)=(5)\cdot(-3)-(-6)\cdot(3)=-15+18 \\ d(A)=3 \end{gathered}`

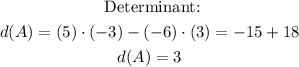
The inverse function is:

`\begin{gathered} A^(-1)=(1)/(\det(A))\begin{bmatrix}{-3} & {-3} & {} \\ {6} & {5} & {} \\ {} & {} & {}\end{bmatrix}=(1)/(3)\begin{bmatrix}{-3} & {-3} & {} \\ {6} & {5} & {} \\ {} & {} & {}\end{bmatrix} \\ A^(-1)=\begin{bmatrix}{-3/3} & {-3/3} & {} \\ {6/3} & {5/3} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-1} & {-1} & {} \\ {2} & {5/3} & {} \\ {} & {} & {}\end{bmatrix} \end{gathered}`

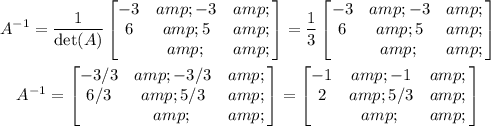
Thus, the solution is:

`\begin{gathered} \begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-1} & {-1} & {} \\ {2} & {5/3} & {} \\ {} & {} & {}\end{bmatrix}\cdot\begin{bmatrix}{8} & {} & {} \\ {-6} & {} & {} \\ {} & {} & {}\end{bmatrix} \\ \end{gathered}`

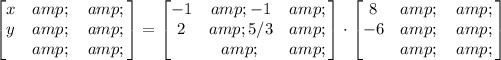
Now, solve the multiplication:

`\begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-1\cdot8+(-1)(-6)} & {} & {} \\ {2(8)+5/3\cdot(-6)} & {} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{-2} & {} & {} \\ {6} & {} & {} \\ {} & {} & {}\end{bmatrix}`