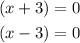Question

Consider the following quadratic equation:x² = 9Step 1 of 2: Using the standard form ax2 + bx + c = 0 of the given quadratic equation, factor theleft hand side of the equation into two linear factors.AnswerKeypadKeyboard Shortcuts= 0

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given quadratic equation.

`x^2=9`

STEP 2: Write the equation in the standard form

`\begin{gathered} \text{standard form}\Rightarrow ax^2+bx+c=0 \\ \text{Given form}\Rightarrow x^2=9 \\ \text{Subtract 9 from both sides} \\ x^2-9=9-9 \\ x^2-9=0 \end{gathered}`

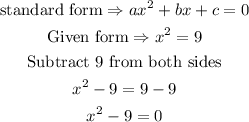
STEP 3: Factor the new quadratic equation into two linear terms

`\begin{gathered} x^2-9=0 \\ \mathrm{Rewrite\: }9\mathrm{\: as\: }3^2 \\ \Rightarrow x^2-3^2=0 \end{gathered}`

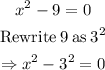
STEP 4: Simplify the equation further

`\begin{gathered} x^2-3^2=0 \\ \mathrm{Apply\: Difference\: of\: Two\: Squares\: Formula\colon\: }x^2-y^2=\mleft(x+y\mright)\mleft(x-y\mright) \\ x^2-3^2=\mleft(x+3\mright)\mleft(x-3\mright)=0 \\ \Rightarrow\mleft(x+3\mright)\mleft(x-3\mright)=0 \end{gathered}`

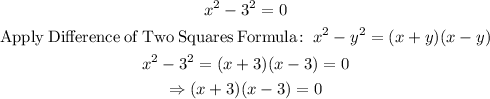
Hence, the factorization of the left hand side of the given quadratic equation will be:

`\begin{gathered} (x+3)=0 \\ (x-3)=0 \end{gathered}`