Question

OGRAPHS AND FUNCTIONSGraphing a parabola of the form y = ax?Graph the parabola.1 2y =4Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right ofbutton.-1210-?10ExplanationCheckTe here to2020 MG

Answer 1

Let us find the vertex point (h, k)

h is the x-coordinate of the vertex point of the equation

`y=ax^2+bx+c`
`h=(-b)/(2a)`

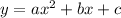
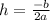
a is the coefficient of x^2,

b is the coefficient of x

From the given parabola

a = 1/4

b = 0

So

`h=(0)/((1)/(4))=0`

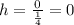
h = 0

k is the y-coordinate of the vertex point, to find it substitute x by h in the equation

`y=(1)/(4)x^2`

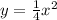
Substitute x by h = 0

`\begin{gathered} k=(1)/(4)(0)^2 \\ k=0 \end{gathered}`

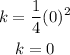
Then the vertex point is (0, 0) ==== the origin point

To find two points on the graph right the vertex point substitute x by 2 positive values greater than 0

We can choose 4 and 8

at x = 4 ===== y = 1/4 (4)^2 = 1/4(16) = 4

The first point on the right side is (4 , 4)

at x = 8 ===== y = 1/4(8)^2 = 1/4(64) = 16

The second point is (8, 16)

We will plot the other points on the left with x = -4 and -8

It will give us the same values of y with the first two points

(-4 , 4) and (-8, 16)

That because (-4)^2 = 16 like (4)^2 = 16

The even powers cancel the negative signs

So we have 5 points to draw the graph

(-8 , 16) , (-4 , 4) , (0, 0) , (4 ,4), (8 , 16)