Question

A 30-foot tree casts a 12-foot shadow as shown inthe picture.30 ftx12Find the angle of elevation to the nearest tenth.12.850°68.2°90°

Answer 1

Since the triangle has a right angle, we can conclude that the diagram is of a right triangle.

When dealing with right triangles, there are some useful formulas that are known as 'Trigonometric Identities'. There are a lot of them but we will need only one of those to solve the problem, that's the equation below:

`\tan (\theta)=(O)/(A)`

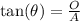
Where θ is the angle, O is the length of the opposite side to the angle, and A the adjacent side to the angle.

Therefore, in the case of our problem,

`\begin{gathered} \theta=x,O=30ft,A=12ft \\ \Rightarrow\tan (x)=(30)/(12)=2.5 \end{gathered}`

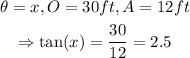
Solving for x, we get

`x=\tan ^(-1)(2.5)=1.1902\text{rad}`

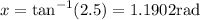
And we can transform radians into degrees,

`\Rightarrow x\approx68.2`

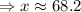
Thus, the answer is the third option. 68.2°