Since the triangle has a right angle, we can conclude that the diagram is of a right triangle.
When dealing with right triangles, there are some useful formulas that are known as 'Trigonometric Identities'. There are a lot of them but we will need only one of those to solve the problem, that's the equation below:
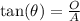
Where θ is the angle, O is the length of the opposite side to the angle, and A the adjacent side to the angle.
Therefore, in the case of our problem,
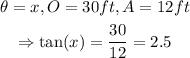
Solving for x, we get
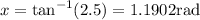
And we can transform radians into degrees,

Thus, the answer is the third option. 68.2°