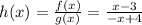Question

Suppose that function h is defined as h(x)=f(x)/g(x).what exactly is the function?

Answer 1

In the graph you can see that f(x) and g(x) are lines, so the first step to know what function is h(x) is to find the functions f(x) and g(x).

Since a single line passes through two points, then to find the functions f(x) and g(x) you can take two points that pass through the graph of each function and obtain the slope, then use the point-slope formula. Then, you have

For f(x)

You can take for example the points (0,-3) and (3,0). Now calculating the slope:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where m is the slope of the line and} \\ (x_1,y_1),(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`
`\begin{gathered} (x_1,y_1)=(0,-3) \\ (x_2,y_2)=(3,0) \\ m=(0-(-3))/(3-0) \\ m=(3)/(3) \\ m=1 \end{gathered}`

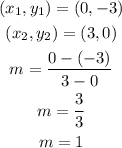
Now using the point-slope formula:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-(-3)=1(x-0) \\ y+3=x \\ \text{Subtract 3 from both sides of the equation} \\ y+3-3=x-3 \\ y=x-3 \end{gathered}`

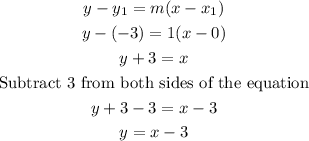
Then, the function f(x) would be

`f(x)=x-3`

For g(x)

You can take for example the points (0,4) and (4,0). Now calculating the slope:

`\begin{gathered} (x_1,y_1)=(0,4) \\ (x_2,y_2)=(4,0) \\ m=(0-4)/(4-0) \\ m=(-4)/(4) \\ m=-1 \end{gathered}`

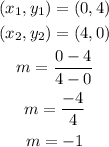
Now using the point-slope formula:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-4=-1(x-0_{}) \\ y-4=-x \\ \text{ Add 4 to both sides of the equation} \\ y-4+4=-x+4 \\ y=-x+4 \end{gathered}`

Finally, the function h(x) will be

`h(x)=(f(x))/(g(x))=(x-3)/(-x+4)`