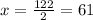First we will label the missing angles of the picture as follows
Note that angles A and B are said to be complementary. So we have the following equation
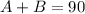
The triangle on the right (the one with the 74) is a isosceles triangle. This type of triangles have the property that the side that connects the sides that have the same length, have the same angles on each corner. So, this leads to
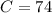
So now, we will find the value of B. To do so, we will use the fact that the sum of the angles of a triangle is 180. So if we apply this fact to the triangle on the right , we get the equation
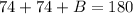
Operating on the left side, we get
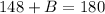
So, by subtracting 148 on both sides, we get
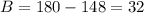
Now, we will find the value of A. To do so, we replace the value of B in the equation we foudn previously, that is.
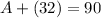
so by subtracting 32 on both sides, we get

Now, notice that the triangle on the left is also an isosceles triangle, so the property we used before also applies. That is
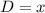
If we apply the sum of the angles property to the triangle of the left, we get
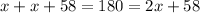
So, if we substract 58 on both sides we get
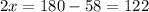
So, by dividing both sides by 2, we get