Question

Identify the oblique asymptote of f(x) = quantity x plus 4 over quantity 3 x squared plus 5 x minus 2.

Answer 1

Answer is no oblique asymptotes

Answer 2

`f(x) = (x + 4)/(3x^(2) + 5x - 2)`

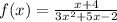
3x² + 5x - 2 = 0
3x² + 6x - x - 2 = 0
3x(x) + 3x(2) - 1(x) - 1(2) = 0
3x(x + 2) - 1(x + 2) = 0
(3x - 1)(x + 2) = 0
3x - 1 = 0 or x + 2 = 0
+ 1 + 1 - 2 - 2
3x = 1 or x = -2
3 3 1 1
x = ¹/₃ or x = -2

f(x) = 3x² + 5x - 2
f(¹/₃) = 3(¹/₃)² + 5(¹/₃) - 2
f(¹/₃) = 3(¹/₉) + 1²/₃ - 2
f(¹/₃) = ¹/₃ - ¹/₃
f(¹/₃) = 0
(x, f(x)) = (¹/₃, 0)

f(x) = 3x² + 5x - 2
f(-2) = 3(-2)² + 5(-2) - 2
f(-2) = 3(4) - 10 - 2
f(-2) = 12 - 12
f(-2) = 0
(x, f(x)) = (-2, 0)

Vertical Asymptotes: ¹/₃ or -2
Horizontal Asymptotes: 0
Oblique Asymptote: No Asymptotes