f(x)=
![\sqrt[3]{x+2}](https://img.qammunity.org/2017/formulas/mathematics/high-school/htsdsf1p9x1jrrvmzlshdqconuhs501yn0.png)
to solve for the inverse of a function you do 4 steps:
1. subsitute f(x) with y
2. switch y and x places
3. solve for y
4. subsitute y with f⁻¹(x)
so we have
f(x)=
![\sqrt[3]{x+2}](https://img.qammunity.org/2017/formulas/mathematics/high-school/htsdsf1p9x1jrrvmzlshdqconuhs501yn0.png)
subsitute f(x) with y
y=
![\sqrt[3]{x+2}](https://img.qammunity.org/2017/formulas/mathematics/high-school/htsdsf1p9x1jrrvmzlshdqconuhs501yn0.png)
switch x and y
x=
![\sqrt[3]{y+2}](https://img.qammunity.org/2017/formulas/mathematics/high-school/gdjwmf6st5xv9udzf0wdarxkqxbq2ckllp.png)
solve for y
x=
![\sqrt[3]{y+2}](https://img.qammunity.org/2017/formulas/mathematics/high-school/gdjwmf6st5xv9udzf0wdarxkqxbq2ckllp.png)
cube both sides
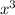
=y+2
subtract 2 from both sides

=y
subsitute y with f⁻¹(x)
f⁻¹(x)=

the answer is f⁻¹(x)=
