Question

n(x) =1+x^2 and m(x) =2-x Given:minimum x and Maximum x: -9.4 and 9.4minimum y and maximum y: -6.2 and 6.2Using the rational function [y=n(x)/m(x)], draw a graph and answer the following: a) what are the zeroes?b) are there any asymptotes? c) what is the domain and range for this function?d) it it a continuous function?e) are there any values of y= n(x)/m(x) that are undefined? Explain

Answer 1

we have the function

`y=(1+x^2)/(2-x)`

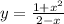
Part a

what are the zeroes?

Solve the quadratic equation in the numerator

x^2+1=0

x^2=-1 -----> the solutions are complex numbers

therefore

the given function has no zeros

Part b

are there any asymptotes?

Remember that the denominator cannot be equal to zero

so

2-x=0

x=2 -----> is a vertical asymptote

Part c

what is the domain and range for this function?

Domain

[-9.4,2) U (2,9.4]

Range

To find out the range, we need to find out the vertex of the rational function

Find out the first derivative of the given function

`y^(\prime)=(-x^2+4x+1)/((2-x)^2)`

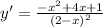
Equate to zero

-x^2+4x+1=0

Solve the quadratic equation

the values of x are

x=-0.236 and x=4.236

Find out the values of y, for that values of x

the points are

(-0.236,0.472) and (4.236,-8.472)

the range is

[0.472,6.2]

Part d

t it a continuous function?

Yes, is a continuous function

Part e

are there any values of y= n(x)/m(x) that are undefined?

No, the function is defined in all its domain

End behavior

In this case, we have that

Degree on Top is Exactly One Greater Than the Bottom

In this case, the graph has a slant asymptote along some line y = mx + b

To find the equation of the line, perform polynomial long division - the quotient gives you

mx + b (the remainder can be ignored)

so

(x^2+1) : (-x+2)

-x-2

-x^2+2x

-------------

2x+1

-2x+4

--------

5

the equation of the slant asymptote is

y=-x-2

therefore

End behavior

x→−∞ y →+∞

x→+∞ y →−∞