Answer:
The entrance fee per parent is $25, while the cost per child is $6.
Explanation:
This problem is solved by using a system of equations.
We know that there are 150 adults and 225 children, which makes a total of $5100. So, the variables here will represent the cost per adult and the cost per children. The first equation is
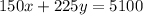
Where
 represents the cost per adult and
represents the cost per adult and
 represents the cost per child.
represents the cost per child.
We also know that the entrance fee of an adult and a child is $31, this means
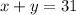
Now, we isolate
 in the second equation, to replace it into the first equation and solve for
in the second equation, to replace it into the first equation and solve for
 , as follows
, as follows
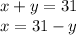
Then,

Now, we use this value to find the other one

Therefore, the entrance fee per parent is $25, while the cost per child is $6.