Question

A planet has a mass of 5.97 x 1024 kg and a radius of 6.38 x 106 m. Find the weight of a 65.0 kg person at 1000 km above the surface of this planet.

Answer 1

To find the weight of a person 1000 km above the surface of a planet, we can use the equation for gravitational force and substitute the given values to calculate the weight in newtons.

Step-by-step explanation:

To find the weight of a person 1000 km above the surface of a planet, we can use the equation for gravitational force:

F = (G * m1 * m2) / r^2

Where F is the force of gravity, G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers.

In this case, the mass of the planet is given as 5.97 x 10^24 kg, the mass of the person is 65.0 kg, and the distance from the planet's surface to the person is 1000 km.

By substituting these values into the equation, we can calculate the weight of the person:

1. Convert the radius from km to m: 1000 km = 1000 * 1000 m = 1,000,000 m
2. Calculate the force of gravity: F = (6.67 x 10^-11 Nm^2/kg^2 * 5.97 x 10^24 kg * 65.0 kg) / (6.38 x 10^6 m + 1,000,000 m)^2
3. Simplify the expression and calculate the weight of the person in newtons.

Answer 2

Answer: The weight of the person above the surface of a planet is 635.83N.

Step-by-step explanation:

To calculate the weight of a person, we use the formula:

`w=mg` ....(1)

where,

w = weight of an object

m = mass of the person = 65kg

g = acceleration due to the gravity of the planet

For the calculation of weight, we need to first find the acceleration due to gravity and for that we use the formula:

`g=(GM)/(r^2)`

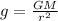
where, g = acceleration due to gravity =
`?m/s^2`

G = Universal gravitational constant =
`6.67* 10^(-11)Nm^2/kg^2`

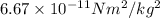
M = mass of the planet =
`5.97* 10^(24)kg`

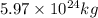
r = distance of the person from the planet =
`6.38* 10^6m`

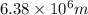
Putting values in above equation, we get:

`g=((6.67* 10^(-11)kgm/s^2.m^2/kg^2)(5.97* 10^(24)kg))/((6.38* 10^6m)^2)\\\\g=9.782m/s^2`

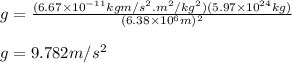
Putting this value in equation 1, we get:

`w=65kg* 9.782m/s^2=635.83N`

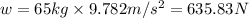
Hence, the weight of the person above the surface of a planet is 635.83N.