Question

Given that the polynomial function has the Given zero, find the other zeros. f(x)=x^3-2x^2-11x+52; -4

Answer 1

The other two zeros are

• 3 + 2i

,

• 3 - 2i

Step-by-step explanation

If the zeros of a polynomial are x1, x2, x3... the polinomial function can be written in a factored form,

`P(x)=(x-x_1)(x-x_2)(x-x_3)\ldots`

Hence, if we know that one of the zeros of f(x) is -4, that means that (x + 4) is a factor. Thus, we can divide the polynomial by that factor,

So f(x) is,

`f(x)=(x+4)(x^2-6x+13)`

To find the other two zeros now we just have to find the zeros of the second factor (x² - 6x + 13), which is much easier because we can simply use the quadratic formula,

`\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this case a = 1, b = -6 and c = 13,

`x=\frac{6\pm\sqrt[]{6^2-4\cdot1\cdot13}}{2\cdot1}`
`x=\frac{6\pm\sqrt[]{36-52}}{2}`
`x=\frac{6\pm\sqrt[]{-16}}{2}`

Note that the number under the radical is negative. Therefore the other two zeros are not real - in other words, in the real numbers set this function has only one zero: -4.

In the complex number set we know that i² = -1, so we can replace the minus sign under the radical by i²,

`x=\frac{6\pm\sqrt[]{16i^2}}{2}`

And solve the square root,

`x=(6\pm4i)/(2)`

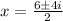
We can distribute the denominator into the sum/subtraction,

`x=(6)/(2)\pm(4i)/(2)`

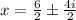
And we get that the other two zeros are,

`\begin{gathered} x_2=3+2i \\ x_3=3-2i \end{gathered}`

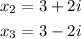
This agrees with the complex conjugate root theorem, which states that