Question

Find an equation of the line containing the centers of the two circles whose equations are given below.x2+y2−4x+6y+4=0x2+y2+6x+4y+9=0

Answer 1

Given the first circle:

x²+ y² − 4x + 6y + 4 = 0

x²+ y² − 4x + 6y = - 4

x² − 4x + 4 + y² + 6y + 9 = - 4 + 4 + 9

(x - 2)² + (y + 3)² = 9

The center of the circle is the point (2, -3) and the radius r = 3

Now, for the second circle:

x² + y² + 6x + 4y + 9 = 0

x² + 6x + 9 + y² + 4y + 4 = - 9 + 9 + 4

(x + 3)² + (y + 2)² = 4.

The center of the circle is the point (- 3, - 2) and the radius r = 2

Finally, we need to find the equation of the line ( y = mx + b), that crosses through the points (- 3, - 2) and (2, -3):

`\begin{gathered} \text{m = }(y_2-y_1)/(x_2-x_1) \\ m\text{ = }\frac{-3\text{ + 2}}{2\text{ + 3}}\text{ = }(-1)/(5) \end{gathered}`

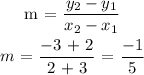
To find b, we replace one point on the linear equation:

y = mx + b

-3 = (-1/5)(2) + b

b = -13/5

So, the equation of the line is:

y = (-1/5)x - 13/5