Question

Find the horizontal or oblique asymptote of f(x) = negative 2 x squared plus 3 x plus 6, all over x plus 2 .

Possible answers:

y = −2x + 7
y = −2
y = 2
y = 2x − 1

Answer 1

`f(x) = (-2x^(2) + 3x + 6)/(x + 2)`

-2x + 7
x + 2|-2x² + 3x + 6
-2x² - 4x
7x + 6
-7x + 14
14x - 8


`f(x) = (-2x^(2) + 3x + 6)/(x + 2) = -(2x^(2) + 3x + 6)/(x + 2) = -2x + 7 + (14x - 8)/(x + 2)`

y = -2x + 7

The answer is A.

Answer 2

Answer: First option is correct.

Explanation:

Since we have given that

`f(x)=(-2x^2+3x+6)/(x+2)`

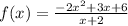
We need to find the horizontal or oblique asymptote .

Since the degree of numerator is more than the degree of denominator.

So, it has oblique asymptote.

`\mathrm{Divide\:the\:leading\:coefficients\:of\:the\:numerator\:}-2x^2+3x+6\mathrm{\:and\:the\:divisor\:}x+2\mathrm{\::\:}(-2x^2)/(x)=-2x\\\\\mathrm{Quotient}=-2x\\\\\mathrm{Multiply\:}x+2\mathrm{\:by\:}-2x:\:-2x^2-4x\\\\\mathrm{Subtract\:}-2x^2-4x\mathrm{\:from\:}-2x^2+3x+6\mathrm{\:to\:get\:new\:remainder}\\\\\mathrm{Remainder}=7x+6\\\\\mathrm{Remainder}=7x+6\\\\=-2x+(7x+6)/(x+2)`

And,

`\mathrm{Divide\:the\:leading\:coefficients\:of\:the\:numerator\:}7x+6\mathrm{\:and\:the\:divisor\:}x+2\mathrm{\::\:}\frac{7x}`
`{x}=7\\\\\mathrm{Quotient}=7\\\\\mathrm{Multiply\:}x+2\mathrm{\:by\:}7:\:7x+14\\\\\mathrm{Subtract\:}7x+14\mathrm{\:from\:}7x+6\mathrm{\:to\:get\:new\:remainder}\\\\\mathrm{Remainder}=-8\\\\Therefore,\\\\(7x+6)/(x+2)=7+(-8)/(x+2)`

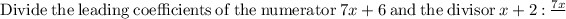
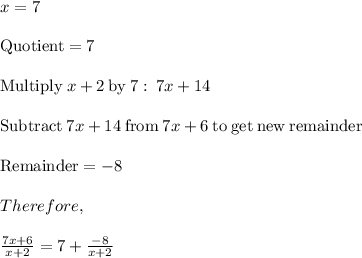
At last, we get,

`-2x+7-(8)/(x+2)`

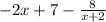
Hence, the oblique asymptote of f(x) is

y=-2x+7

Therefore, First option is correct.