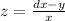According to the given data we have the following equation:
zx+y=dx
To solve for the variable z the equation we would make the following steps:
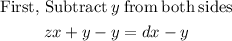
Next we would have to simplify the equation above, so:
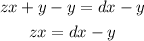
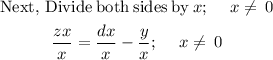
Therefore, the final result by dividing bith sides by x we would get the following for z: