Question

Given u = −5i + 8j and v = 56i + 35j, are u and v parallel or orthogonal? Explain.

Answer 1

Step-by-step explanation

Two vectors are orthogonal if the dot product of the vectors is zero. On the other hand, the dot product of two vectors is defined as follows:

`\begin{gathered} u=\langle u_1,u_2\rangle \\ v=\langle v_1,v_2\rangle \\ u\bullet v=u_1v_1+u_2v_2 \end{gathered}`

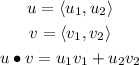
So, let us calculate the dot product of the given vectors:

`\begin{gathered} u=-5i+8j\Rightarrow u=\langle-5,8\rangle \\ v=56i+35j\Rightarrow v=\langle56,35\rangle \\ u\bullet v=-5*56+8*35 \\ u\bullet v=-280+280 \\ u\bullet v=0 \end{gathered}`

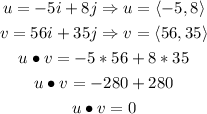
As we can see, the dot product of the given vectors is zero. Therefore, the vectors are orthogonal.

Answer

The vectors are orthogonal because u · v = 0.