Question

A circle with radius 12 mm divided into 20 sectors of equal area. Which is the area of one sector to the nearest tenth?

Answer 1

The area of a full circle is (pi) (radius²)

= (pi) (12 mm)² = 144π mm²

1/20 of that is (0.05) x (144π mm²)

= 7.2π mm² = 22.6 mm² .

Answer 2

Answer: The area of one sector is 22.6 sq. mm.

Step-by-step explanation: Given that a circle with radius 12 mm divided into 20 sectors of equal area.

We are to find the area of one sector to the nearest tenth.

The AREA of a circle with radius 'r' units is given by

`A=\pi r^2.`

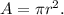
Here, the radius of the circle is

r = 12 mm.

Therefore, the area of the circle will be

`A=\pi r^2=(22)/(7)* (12)^2=(22* 144)/(7)=452.57~\textup{sq. mm.}`

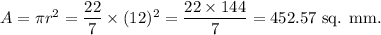
Since the whole circle is divided into 20 equal sectors.

So, the area of one sector is

`A_s=(1)/(20)* 452.57=22.62\sim 22.6~\textup{sq. mm.}`

Thus, the area of one sector is 22.6 sq. mm.