ANSWER
11.02 m/s
Step-by-step explanation
Given:
• Your mass, m = 62 kg
,
• Your initial velocity, u = 0 (you start from rest at the top)
,
• The coefficient of kinetic friction between you and the slide, μk = 0.12
,
• The angle between the slide and the horizontal, θ = 84°
,
• The length of the slide, d = 6.3 m
Let's make a diagram of the description of the slide given,
First, we can find what is your gravitational potential energy just before the floor is retracted,
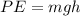
We can find the vertical height of the slide using the right triangle formed,
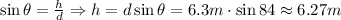
So your gravitational potential energy is,
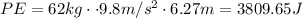
If there was no friction between you and the slide, this energy would be conserved and it would be equal to your kinetic energy when you reach the bottom of the straight portion of the slide. However, there is indeed friction, so some of this energy will be lost to the work done by the kinetic frictional force.
To find the mentioned work, we have to draw a force diagram of you sliding down the slide and find the kinetic frictional force,
By Newton's second law,
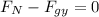
Using trigonometry, we have that the weight in the y-direction is,
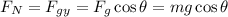
So, the frictional force is,
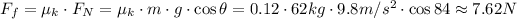
And this force acts for a distance of 6.3 meters, so the work it does on the person sliding down the slide is,
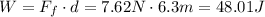
This is the energy lost to friction, so the kinetic energy you will have at the end of the straight portion of the slide is,

This kinetic energy is equal to,

Solving for v,

Hence, your speed at the end of the straight portion of the slide is 11.02 m/s, rounded to two decimal places.