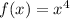Question

Graph a 4th degree or higher polynomial function whose graph never cross the horizontal axis more than once

Answer 1

`f\mleft(x\mright)=x^4`

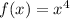
Explanation:

The Fundamental Theorem of Algebra states that the degree of a polynomial is the maximum number of roots the polynomial has.

For polynomials, the degree of the polynomial represents how many times the function crosses the x-axis or the zeros it has. Then if we want to graph a 4th degree or higher polynomial that crosses the horizontal axis no more than once:

`f\mleft(x\mright)=x^4`