Given the scores on a statewide standardized test are normally distributed
Mean = μ = 78
Standard deviation = σ = 3
Normalize the data using the z-score by using the following formula and chart:
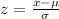
Estimate the percentage of scores of the following cases:
(a) between 75 and 81
so, the z-score for the given numbers will be:
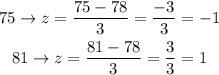
As shown, the percentage when (-1 < z < 1) = 68%
(b) above 87
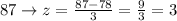
The percentage when (z > 3) = 0.5%
(c) below 72
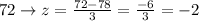
The percentage when (z < -2) = 0.5 + 2 = 2.5%
(d) between 75 and 84
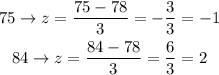
The percentage when ( -1 < z < 2 ) = 68 + 13.5 = 81.5%