Question

The mean of the distribution is 77.3 and the standard deviation is 4.8

Answer 1

In statistics, the 68–95–99.7 rule, also known as the empirical rule, is a shorthand used to remember the percentage of values that lie within an interval estimate in a normal distribution: 68%, 95%, and 99.7% of the values lie within one, two, and three standard deviations of the mean, respectively.

Given:

From the given curve, we can assume the extreme values are three standard deviations of the mean since the shaded area covers almost all parts of the curve i.e :

`z\text{ =3 or -3}`

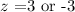
Using the formula for z-score, we can find the extreme points:

`\begin{gathered} z\text{ = }(x-\psi)/(\sigma) \\ \text{where }\psi\text{ is the mean and} \\ \sigma\text{ is the standard deviation} \end{gathered}`

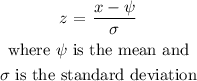
Substituting we have:

`\begin{gathered} 3\text{ =}(x_1-77.3)/(4.8) \\ x_1-77.3=14.4 \\ x_1\text{ =91.7} \end{gathered}`
`\begin{gathered} -3\text{ = }(x-77.3)/(4.8) \\ x-77.3\text{ = -14.4} \\ x\text{ =62.9} \end{gathered}`

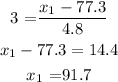
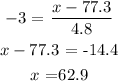
Hence,

The percentage of total area shaded is 99.7%

The left and right values are 62.9 and 91.7 respectively