Question

Solve each of these equations. 2(x+5)= 3x + 1 3y - 4-0 y = 3(n + 2) = 9(6. n)

Answer 1

Let's solve each of the given equations.

• Equation 1:

2(x + 5) = 3x + 1

Let's solve for x using the following steps:

Step 1:

Apply distributive property to the left hand side of the equation

2(x) + 2(5) = 3x + 1

2x + 10 = 3x + 1

Step 2:

Sutract 10 from both sides

2x + 10 - 10 = 3x + 1 - 10

2x = 3x - 9

Step 3:

Subtract 3x from both sides of the equation

2x - 3x = 3x - 3x - 9

-x = -9

Step 4:

Divide both sides by -1

`\begin{gathered} (-x)/(-1)=(-9)/(-1) \\ \\ x=9 \end{gathered}`

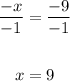
• Equation 2:

3y - 4 = 6 - 2y

Let's solve for y.

Add 4 to both sides:

3y - 4 + 4 = 6 + 4 - 2y

3y = 10 - 2y

Add 2y to both sides:

3y + 2y = 10 - 2y + 2y

5y = 10

Divide both sides by 5:

`\begin{gathered} (5y)/(5)=(10)/(5) \\ \\ y=2 \end{gathered}`

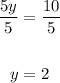
• Equation 3:

3(n + 2) = 9(6 - n)

Let's solve for n.

Apply distributive property:

3(n) + 3(2) = 9(6) +9(-n)

3n + 6 = 54 - 9n

Subtract 6 from both sides:

3n + 6 - 6 = 54 - 6 - 9n

3n = 48 - 9n

Add 9n to both sides:

3n + 9n = 48 - 9n + 9n

12n = 48

Divide both sides by 12:

`\begin{gathered} (12n)/(12)=(48)/(12) \\ \\ n=4 \end{gathered}`

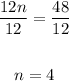
ANSWER:

• x = 9

• y = 2

• n = 4