Question

How many different 6-letter words can be madea. if the first letter must be C, X, Q, or M and no letter may be repeated?b. if repeats are allowed (but the first letter is C, X, Q, or M)?c. How many of the 6-letter words (starting with C, X, Q, or M) with no repeats endin R?a. If the first letter must be C, X, Q, or M, and all the letters in the word must be different, then there are6-letter words.

Answer 1

First let;s solve part (a)

Now first place can be filled in 4 ways

Second place can be filled in 22 ways

Third place can be filled in 21 ways

Fourth place can be filled in 20 ways

Fifth place can be filled in 19 ways

Sixth place can be filled in 18 ways

So total number of 6 letter words will be

`\begin{gathered} 4*22*21*20*19*18 \\ =12,640,320 \end{gathered}`

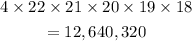
(b)

If digits are can be repeated then first pace can be filled in 4 ways but trest of the positions can be filled in 26 way s

So total numbe rof words will be

`\begin{gathered} 4*26*26*26*26*26 \\ =47,525,504 \end{gathered}`

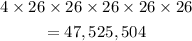
c) Now first place can be filled in 4 ways

And sixth place can be fille din 1 way only

and no letter can be repeated

So second place can be filled in 21 ways

Third place can be filled in 20 ways

Fourth place can be filled in 19 ways

Fifht place can be filled in 19 ways

So total numbe of words will be

`\begin{gathered} 4*21*20*19*18*1 \\ =574,560 \end{gathered}`

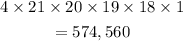
The last part is same as the part (a)