a.
The mean of a sample is given by:
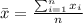
In this case we have:

Therefore, the mean of the sample is 7
The standard deviation is:
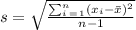
Then we have:
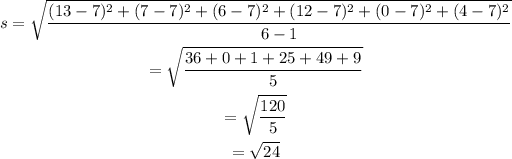
Therefore, the standard deviation is √24
b.
The standard error is defined as:
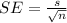
Then we have:
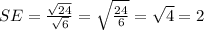
Therefore, the estimated standard error is 2